Overview of Difference Tables and Difference Fans
Difference tables have been studied since the days of Gauss and Newton. Although surprisingly simple, they display some interesting patterns dealing with finite differences. Conway and Guy give a brief overview of difference tables in "The Book of Numbers". One aspect that we will be focusing on will be a special difference table called a Jackson Difference fan.
Suppose we have a sequence of numbers that we want to derive a formula for (or even calculate the next term in the sequence). For this we might construct a difference table where every number is the difference between the two right above it (right minus left). An example with the sequence for 3n would look like the following: (Note : Some texts display difference tables from left to right. For our discussion, however, we will be using a top to bottom notation - like an inverted pyramid. The results are still the same).
1 3 27 81 243 729 2187 6561 19683
...
2 24 54 162 486 1458 4374 13122
22 30 108 324 972 2916 8748
8 78 216 648 1944 5832
70 138 432 1296 3888
68 294 864 2592
226 570 1728
344 1158
814
Table
1
In the second row, the values are 3-1=2, 27-3=24, 81-27=54 and so on. The same process is repeated for the rows that follow. All of this might not seem too interesting until we determine what these repetitive differences tell us about our number sequence.
Some interesting patterns can arise in different tables. Here are a few
examples. The sequence in the following table represents the maximum number of regions obtained by joining n points around a circle by straight
lines. It's not really important that you understand the sequence right now. We
are just using it to generate some numbers.
1 2 4 8 16 31 57 99 163
...
1 2 4 8 15 26 42 64
1 2 4 7 11 16 22
1 2 3 4 5 6
1 1 1 1 1
0 0 0 0
0 0 0
0 0
0
Table 2
Here is a difference table for the sequence n4.
0 1 16 81 256 625 1296 2401 4096
...
1 15 65 175 369 671 1105 1695
14 50 110 194 302 434 590
36 60 84 108 132 156
24 24 24 24 24
0 0 0 0
0 0 0
0 0
0
Table 3
The following is a difference table for the polynomial sequence 4n3 -
3n2 + 2n + 6
6 9 30 93 222 441 774 1245 1878
...
3 21 63 129 219 333 471 633
18 42 66 90 114 138 162
24 24 24 24 24 24
0 0 0 0 0
0 0 0 0
0 0 0
0 0
0
Table 4
Notice there is a row of constant numbers in each of the last three examples. This will be discussed in the next section.
To understand why we are getting a row of constants let us first consider
what happens if the sequence we are starting with is a polynomial sequence. A polynomial has
the general form:
qnxn + ... + q2x2 + q1x +
q0
Something interesting happens when we subtract two consecutive sequence
values that are both derived from a polynomial equation. For example if we start with a third order polynomial (q3x3
+ q2x2 + q1x + q0) the difference
between two terms in the sequence, using a little algebra to combine like terms,
would be a second order polynomial :
q3x3
+ q2x2 + q1x + q0 q3(x+1)3
+ q2(x+1)2 + q1(x+1) + q0
3q3x2 + (2q2 + 3q3)x
+ q1 + q2 + q3
Similarly, starting with a second order polynomial (q2x2 +
q1x + q0), the difference is is a first order polynomial:
q2x2
+ q1x + q0 q2(x+1)2
+ q1(x+1) + q0
2q2x
+ q1
+ q2
Not surprisingly, if we start with a first order polynomial (q1x + q0),
our difference is a constant (i.e. an order of zero):
q1x + q0 q1(x+1) + q0
q1
The same reduction in order occurs for polynomials whose order is greater than
three as well. We can therefore conclude that any polynomial sequence in a
difference table with an order of (n) will be reduced to a row or constants in
(n) steps. This can be verified from the examples above.
The row of constant numbers mentioned previously has another use as well. If we assumed that this sequence continues on forever, we can calculate "backwards" using addition from the bottom-up to find the next term in the sequence. For Table 3, the next term would be calculated using the following steps:
... 2401 4096 6561
= 4096 + 2465
... 1105 1695 2465
= 1695 + 770
...
434 590 770
= 590 + 180
... 132 156 180
= 156 + 24
... 24 24 24
(assume constant)
^
|---
Start from the bottom and work upwards by adding
This process might come in handy then next time you are trying to guess the next number in a sequence for a brain teaser.
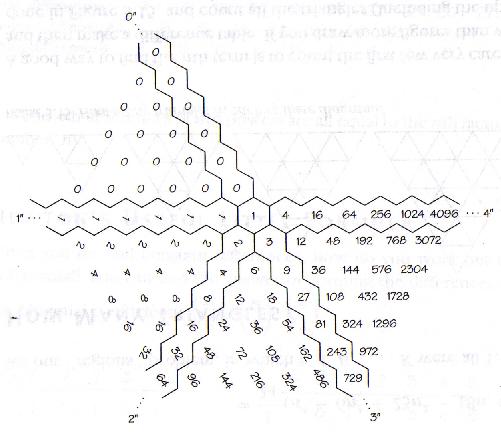
Conway and Guy mention Jackson Difference Fans and note an interesting phenomenon that can be discovered by using the sequence along the left hand side of the table.
"Robert Jackson suggests that if you've completed a difference table and still don't understand the sequence, you should turn the paper through an angle of 60 degrees, say, and start again and perhaps repeat this several times to make a fan of difference tables. Jackson found that the fanning process converts powers of 4 to powers of 3 to powers of 2 to powers of 1 to powers of 0. (see figure below). In general a sequence kn, multiplied by any polynomial in n, is reduced to zeros by a k-fold difference fan."

Figure 1
To understand why this occurs let us first consider how a difference table works. For
now we will refer to the horizontal lines (i.e. a0, a1,
... ai) as rows and the diagonal lines (i.e. a0, b0,
c0 ...zi) as "columns". The notation for rows and columns will start
at 0. Thus a standard difference table looks like the following:
a0 a1 a2 a3
a4 ... row
0
b0 b1 b2
b3 ... row
1
c0 c1
c2 ... row
2
d0 d1 ...
e0
...
. . .
c c c
o o o
l l l
0 1 2
We can see that all of the values below can be calculated from values in the
first row.
b0
= a1 - a0
b1
= a2 - a1
b2 = a3 - a2
b3 = a4 - a3
c0 = b1 -
b0 = a2 - 2a1 + a0
c1 = b2 - b1 = a3 - 2a2
+ a1
c2 = b3 - b2 = a4 - 2a3
+
a2
d0 = c1 -
c0 = a3 - 3a2 + 3a1 - a0
d1 = c2 -
c1 = a4 - 3a3 + 3a2 - a1
e0 = d1 - d0 = a4 - 4a3 +
6a2 - 4a1 + a0
If we suppose our sequence on the top line is a number
raised to
a power (kn). In this case, n will be our starting exponent. The top line then becomes:
kn kn+1 kn+2 kn+3
kn+4 ...
Substituting these back into the previous equations for b0, c0,
d0, e0, (i.e. the left hand column of the table) we get:
b0 = kn+1 - kn = kn(k-1)
c0 = kn+2 - 2kn+1 + kn
= kn(k-1)2
d0 = kn+3 - 3kn+2 + 3kn+1
- kn = kn(k-1)3
e0 = kn+4 - 4kn+3 + 6kn+2
- 4kn+1 + kn = kn(k-1)4
Thus the general equation for the first column can be summed up as the
following:
(1)
X0 = kn(k-1)r
r is the row number starting at 0, n is the starting exponent and X0
represents a0, b0, c0...
As an interesting side note, we can use the same methods as above to calculate
a general equation for sequence a1, b1, c1...
(2)
X1 = kn+1(k-1)r
Now let us carry this a step forward and derive a general formula for any row
and column. This means we can calculate any value in the table given the
starting exponent (n). The general equation looks like the following:
(3)
Xc = kn+c(k-1)r
c is the column number starting at 0.
We started out wanting to understand why the left hand column reduces powers of
(n) to powers of (n-1) to powers of (n-2) and so on. Using formula (3) and
setting c = 0, (i.e. the left most column) we are back to formula (1). In
order for this to work properly, our starting exponent (n) needs to be 0 (i.e. 40).
This gives us:
X0 = k0(k-1)r = (k-1)r
By taking the left most column and starting a new difference table (i.e. turning the paper through
an angle of 60 degrees), we are right back where we started in the first place
(except the base value has now been reduced by one). In
our new sequence, the row (r) values will be 0, 1, 2,... which is essentially
what the starting exponent (n) did in the original sequence. The transformation
for all of this can be represented as follows:
kn -> (k-1)n
Because our value k is being reduced by one each time, our entire table will be reduced to zeros in k-steps. Other interesting observations can be made by repeating for more than k-steps (the numbers start to go into negative values) or by calculating a Jackson fan when the starting exponent isn't zero.
Conway, J. H. and Guy, R. K. "Jackson's Difference Fans". The Book of
Numbers. pp. 84-85, 1996.
Weisstein, Eric W., "Jackson's Difference Fans." Eric Weisstein's World of Mathematics.
http://mathworld.wolfram.com/JacksonsDifferenceFan.html, 1999.